ontwerpen waarbij de overgang tussen verschillende segmenten van een oppervlak meer continu zijn geven in het algemeen inderdaad een betere kwaliteitsperceptie.
bvb, met dank aan
http://bentonian.com/Lectures/FGraphics1920/4. Beziers, B-Splines and NURBS.pdf:

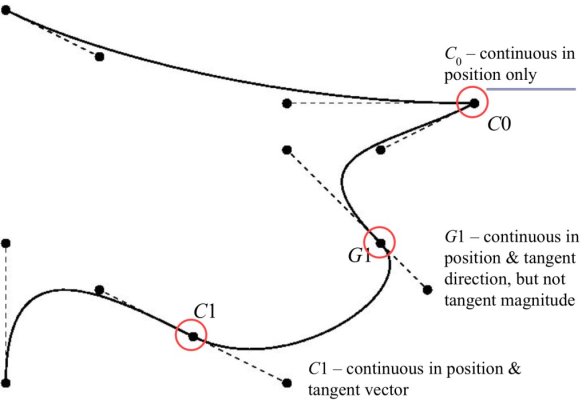
wiskundig gezien wil je minstens G1-continuïteit hebben in de overgang tussen 2 segmenten.
dat betekent dat de 2 segmenten door hetzelfde punt gaan + dezelfde richting hebben in dat punt. als je met cirkelsegmenten en rechte stukken werkt krijg je dat prima voor mekaar met houtje touwtje methodes.
bvb wil je een cirkelsegment met R=3000mm koppelen aan een cirkelsegment met R=2000mm, dmv een segment met R=250mm, dan teken je vanuit het middelpunt van de cirkel R=3000 een 2de cirkel met R2750 (3000-250) en vanuit het middelpunt van de cirkel met R=2000 een 2de cirkel met R1750 (2000-250).
waar de 2 kleinere cirkels snijden ligt het middelpunt voor de R250 cirkel.
de lijn door de middelpunten van de R3000 en de R250 snijdt beide cirkels waar ze mekaar raken en loodrecht daarop ligt de gemeenschappelijke raaklijn.
met Beziers, B-splines, NURBS, … kan je hogere continuïteit verwezenlijken (bvb dat de kromming gelijk is aan beide kanten) maar die lijken mij in de praktijk niet zo toepasbaar in de houtbewerking tenzij je een CNC hebt.