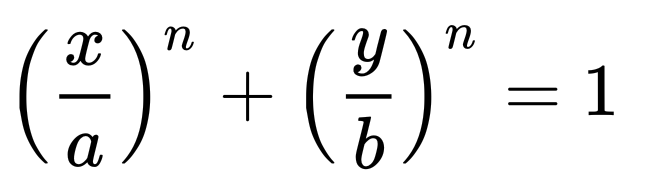Deens ovaal

[Musicus]

Heel mooi gedaan zeg! Past ook heel chique met dat notenhout.

Ik zal het maar verklappen, maar dit is geen notenhout.. Het is thermisch verduurzaamd Fraké en dat lijkt er heel erg op qua kleur en tekening. Ik had het nog liggen van wat buitenmeubels die ik laatst had gemaakt. Ik heb er eerder al 2 kinderstoeltjes van gemaakt en dat werkte prima. Het is alleen wat brozer dan hout wat niet thermisch is verduurzaamd. Als je daar rekening mee houdt gaat het prima.

Voordeel is dat het veel en veel goedkoper is dan notenhout....

 

[Guido76]

Dit staat bij mij ook op de planning. Een tafel zo als Ernst Kuhne heeft gemaakt. Ik heb een notenhouten tafelblad 4 cm dik van 2.20 lang en 1000 breed.

Maar als ik zijn tafel bekijk begrijp ik niet hoe hij op een radius van 250 cm uit komt.

Ik heb een plaatje gevonden met maten erop, en een collega van mij heeft de formule in excel gezet.

Ik kom voor mijn tafel op een radius van 4.80 mtr voor de lange zijde. De korte zijde komt op 0.75 meter.

 

[henkverhaar]

Als ik naar je plaatje kijk dan is, visueel, R kleiner dan c. Als c 1950 mm is kan R toch nooit 4803 mm zijn? Ik denk dat er iets niet in orde is met je formule... Of met het plaatje natuurlijk...

 

[Guido76]

Het plaatje is niet gegenereerd door de uitkomst van de formule maar enkel een visuele verduidelijking voor wat je moet invullen bij de formule.

Het bovenste plaatje vond ik bij een meubelmaker welke deens ovalen tafels aanbiedt. Hier dus de waardes uitgehaald hoe hun 220x100 cm tafel aan afmetingen heeft. Dit geeft een radius van 4.8 meter.

 

[jorisvh]

de formule klopt en geldt voor een cirkelsegment.
vertrekken van d+h=R en d^2=(c/2)^2=R^2 en wat herschikken geeft R=h/2+c^2/(8h), QED.
afhankelijk van de openingshoek theta kan c (de koorde) voor een bepaalde straal R varieren tussen 0 (0gr) en 2R (180gr).

 

[henkverhaar]

de formule klopt en geldt voor een cirkelsegment.
vertrekken van d+h=R en d^2=(c/2)^2=R^2 en wat herschikken geeft R=h/2+c^2/(8h), QED.
afhankelijk van de openingshoek theta kan c (de koorde) voor een bepaalde straal R varieren tussen 0 (0gr) en 2R (180gr).

Ja, die volg ik.

Ik denk dat het punt is dat de tafel van ernst veel 'ronder' is dan het ontwerp van Guido... Die straal die je uitrekent heeft niet direct iets met de grootte van de tafel te maken maar vooral met de kromming van de zijden?

 

[jorisvh]

vermits een Deens ovalen tafel vast wel eens op mijn planning komt, ben ik alvast even in de theorie gedoken.
van de term Deens ovaal vind ik geen duidelijke definitie maar ik veronderstel zoals anderen hierboven dat het wiskundig gezien om een superellips gaat en dat de naam voortkomt uit het gebruik door Piet Hein (Deen).

theorie over superellips:

Superellips - Wikipedia

nl.wikipedia.org

Superellipsen | Wiskunde is leuk

formule:

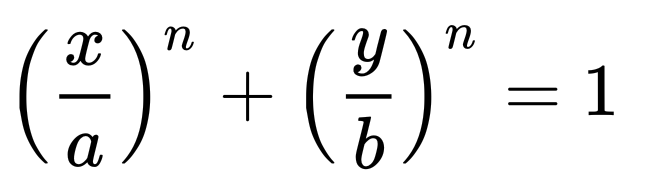
met n=2 wordt dit een ellips. met daarenboven a=b een cirkel.
hoe groter n, hoe meer het een rechthoek (of vierkant) wordt.

Piet Hein heeft ze o.a. gebruikt als grondplan van een verkeersknooppunt in Stockholm.

en voor de Fritz Hansen superellips tafel.

welke waarde van n, a, b voor de tafel gebruikt zijn, vind ik nergens.

deze superellipsen lijken mij moeilijk te maken tenzij je de curve in een CNC kan programmeren.
een constructie met spijkers en een stang of touw komt op 1 of andere manier neer op een som van lengtes die constant blijft en, gezien de stelling van Piet Agoras, wordt dat dus iets met sommen van kwadraten, maw n=2, maw ellipsen of cirkels.

wat @Musicus gedaan heeft met 4 spijkers op de hoekpunten van een rechthoek en een touw komt neer op ellips segmenten aan elkaar breien. een volledige ellips teken je met 2 spijkers en een touw. hier wordt telkens een ander paar spijkers ‘geactiveerd’ als brandpunten (2 op de lange zijde -> 2 op de diagonaal -> 2 op de korte zijde -> …).

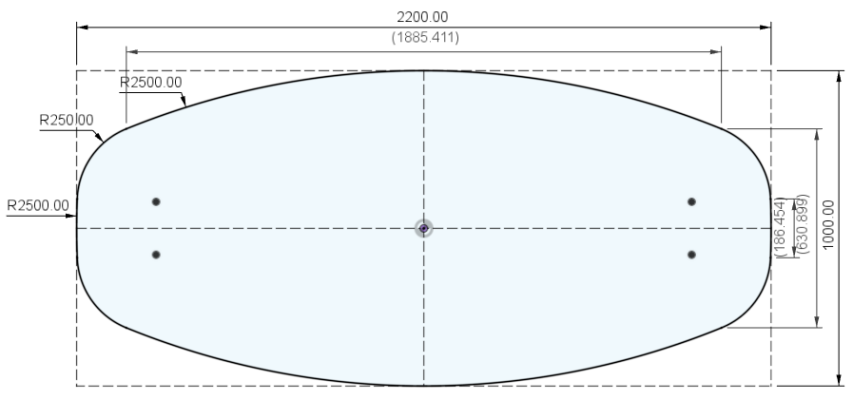
de tafel van @ErnstKuhne bestaat uit 4 cirkelsegmenten met identieke straal 2.500mm, binnen een rechthoek van 2.500x1.250mm met "hoeken" afgerond met cirkelsegmenten van 250mm.
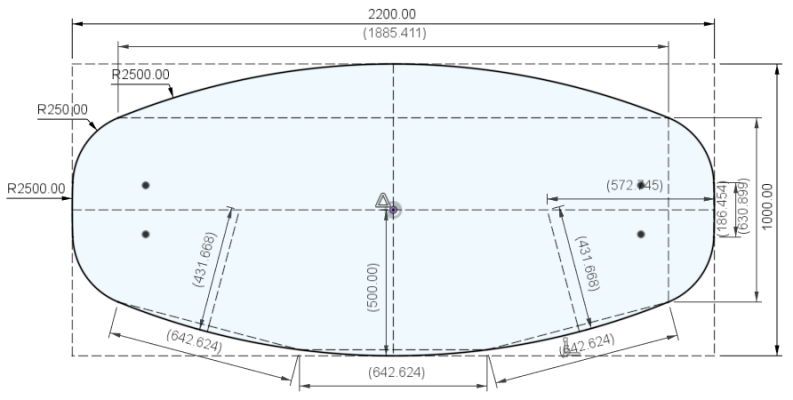
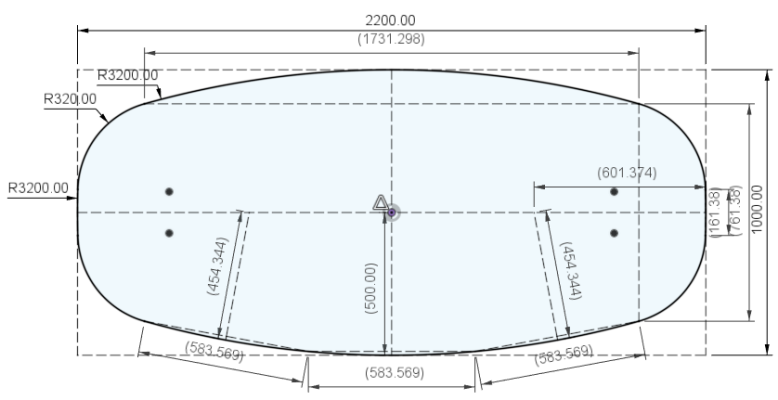
zonder CNC lijkt zo’n een benadering met cirkelsegmenten mij het makkelijkst omdat je die met een freespasser kan maken.

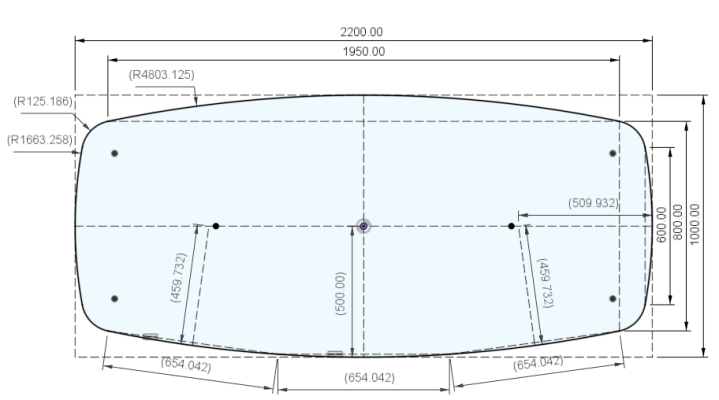
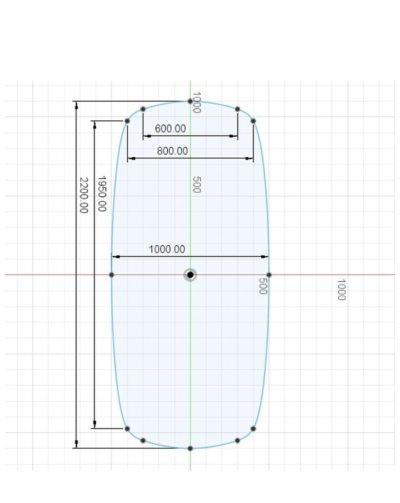
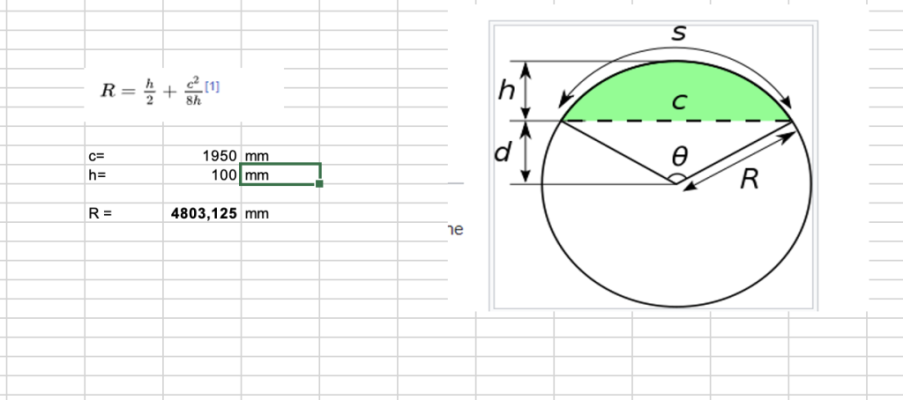
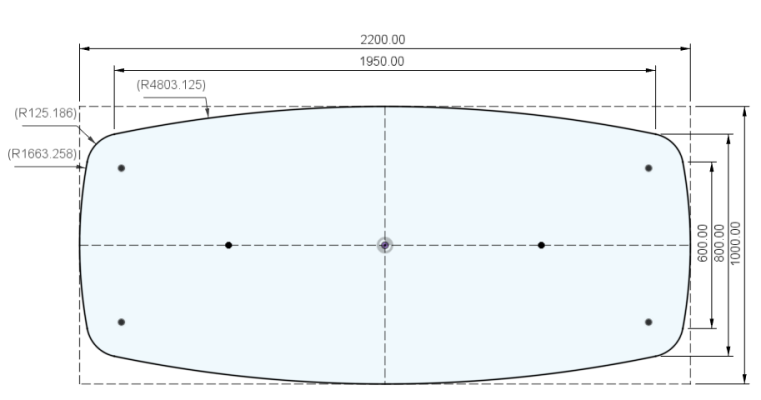
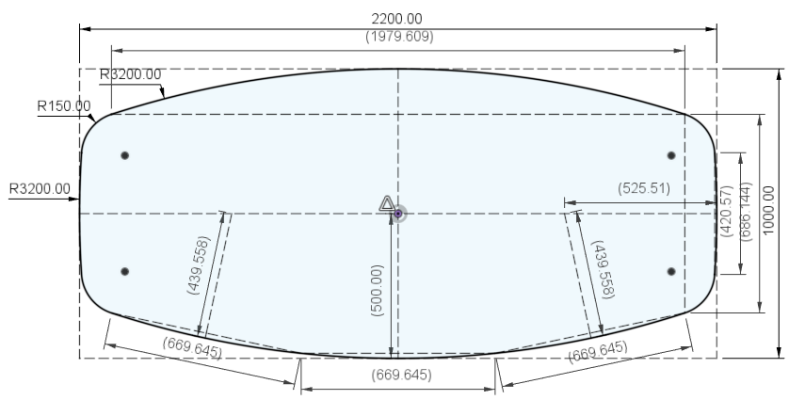
de Fusion360 schets van @Guido76 bestaat ook uit cirkelsegmenten en vertrekt van vastgelegde c=1.950 en h=100 voor de lange zijde en c=600 voor de korte, binnen een rechthoek van 2.200x1.000mm. daaruit volgen de stralen van de cirkelsegment, in dit geval verschillend voor de lange (~4800mm) en korte (750?, lijkt mij op zicht meer) kanten.

ik ga morgen eens proberen om deze varianten te tekenen op computer, dan wordt het wellicht wat duidelijker.

 

[Guido76]

Ja, die volg ik.

Ik denk dat het punt is dat de tafel van ernst veel 'ronder' is dan het ontwerp van Guido... Die straal die je uitrekent heeft niet direct iets met de grootte van de tafel te maken maar vooral met de kromming van de zijden?

Ja, die tafel van Ernst is inderdaad wel ronder. Maar hij had ook een langer en breder tafelblad tot zijn beschikking.

De vorm Deens Ovaal is wellicht minder feitelijk dan een cirkel of vierkant, dus meer naar eigen inzicht interpreteerbaar.

Ik heb een blad van 220 x 100 tot mijn beschikking. Wil ik de lange zijde een ronding geven die 10 cm naar binnen valt komt ik uit op deze radius. Zo maak ik wel maximaal gebruik van mijn blad.

Ik ga het eerst op mdf plaat uittekenen. Dan kan ik de radius nog een beetje aanpassen. De kopse kanten en hoeken zal ik dan ook pas ter plekke een beetje uittekenen met een touwtje. Gewoon een beetje spelen met de radius zodat er een elegante vorm uitkomt.

Het heeft dan eigenlijk min of meer de vorm van een elips met afgeplatte punten. Of het wiskundig klopt maakt mij eigenlijk niet uit.

Wat mij wel uit maakt is hoe ik die vorm in een plaat mdf krijg. En het meest zuivere zou een CNC zijn maar die heb ik niet. Daarna komt dus een bovenfrees aan een lange lat en een vast draaipunt. Zoiets kun je dan ook reproduceren voor de andere zijde.

In plaats van met een touwtje dit uit te proberen heb ik mijn collega gevraagd dit uit te rekenen in autocad en hij kwam met dit excel sheetje op de proppen. Ik kan nu voor elke maat de radius uitrekenen.

 

[jorisvh]

het eten smaakt niet beter als de tafel voldoet aan een wiskundige formule .

heb het "plaatje van de meubelmaker" even in Fusion360 gestoken en blijkt dat de maten alles 100% bepalen. de stralen worden:

• 4.803mm lange zijde
• 1.663mm korte zijde
• 125mm afrondingen

de maten zonder () zijn gekozen, de maten met () volgen daaruit.

een cirkel met straal van 4m80 frezen met een freespasser is nog een uitdaging maar moet lukken (als je atelier groot genoeg is tenminste).

de afrondingsstralen van de tafel van Ernst binnen zijn te klein voor een tafel van 2200x1000. de ronding is te groot waardoor er aan de kopse kant onvoldoende zitbreedte overblijft.

 

[Guido76]

Fantastisch!! Hier kunnen we wat mee. En wat wel blijkt, het is een vorm waar je nog zelf een beetje mee kunt spelen.

De rondingen op de kopse kanten kun je nog een beetje meer of minder rond maken.

Hoe zit het plaatje eruit als je de gulden middenweg neemt?

Mijn plaatje is met Straal 4.8 meter. De tafel van Ernst 2.5 meter. Dus ergens een straal van 3.2 meter bijv?

En zo kun je dus allerlei kanten op. Ook hoe de ruimte in huis is.

De tafel van Ernst toegepast op een blad van 220 geeft dan minder kopse kant ruimte, maar het lijkt dat het nog best wel te doen is voor als er een keer iemand aanschuift. Niet als permanente volwaardige eetplek, maar visite of een kind kan prima.

Maar nu het geheel overbrengen op een tafel, liefst niet uit het handje. Dus toch die frees aan een lange stok/plank.

In mijn garage lukt dat ook niet omdat die te vol staat. Maar buiten op het terras gaat wel, of voor op de oprit. Of bij de buurman onder de carport.

Enkel wachten op een beetje fatsoenlijk weer.

 

[Bert Vanderveen]

Je moet natuurlijk wel rekening houden met de ergonomie. Dus hoeveel stoelen/zitplaatsen heb je nodig en dan rekenen op toch wel 70 cm per plek.

Als het gaat om de uitwerking heb ik nog een tip: gebruik stucstop of stevig papier afgeknipt tot de buitenmaat. Vouw in vieren (dus 1 keer overlangs en 1 keer dwars). Teken nu de krommen, dat kan met behulp van gebogen latten. Heb je dat voor elkaar, schoon afsnijden of knippen. Uitvouwen en de overgangen verfijnen.
Dit als model gebruiken, dus.

 

[Guido76]

Ja, het juiste formaat en ergonomie is wel van belang.

Het op papier uitknippen vindt ik zelf toch niet handig. Want dan moet je het van papier alsnog weer overbrengen op het hout. En dan met decoupeerzaag, schaven en schuren?

Dan lijkt mij de bovenfrees toch handiger om direct een strakke en zuivere mal te maken.

 

[Dirkie]

Ik heb een tijdje terug een tafel gemaakt die ook op basis van cirkel segmenten ontworpen was. Toen heb ik een kwart mal uit 9mm MDF gemaakt. De cirkelsegmenten op de mal uitgezet door middel van een stuk touw en een potlood en een hulpplankje met een spijker. Je stelt de gewenste radius in door de afstand tussen het plankje en het potlood (lusje in het touw) op de lengte van de radius te maken. Plankje vastklemmen, MDF netjes haaks verderop leggen, cirkelsegment tekenen. Daarna netjes uitzagen en afwerken. Dan kan je met een kopieerfrees / kopieerring elke keer een kwart tafel uitfrezen.

 

[Dirkie]

Ik heb nog een foto van het frezen gevonden. Vriend voor wie de tafel was even subtiel anoniem gemaakt...

 

[jorisvh]

Hoe zit het plaatje eruit als je de gulden middenweg neemt?
Mijn plaatje is met Straal 4.8 meter. De tafel van Ernst 2.5 meter. Dus ergens een straal van 3.2 meter bijv?
De tafel van Ernst toegepast op een blad van 220 geeft dan minder kopse kant ruimte, maar het lijkt dat het nog best wel te doen is voor als er een keer iemand aanschuift. Niet als permanente volwaardige eetplek, maar visite of een kind kan prima.

komt er op neer dat je (voor gegeven buitenafmetingen) 3 maten kan kiezen en dat de rest volgt daaruit. in het eerste vb hierboven heb ik 3 lengtes gekozen om de stralen te bepalen, in het 2de de 3 stralen.
ergonomisch gezien zou ik voor een dagelijkse eetplek mikken op:

• zitbreedte: min 60cm, liever 70cm
• beenruimte (rand tafel tot midden): min 40cm, liever 50cm

voor een kind of voor af en toe kan het wat krapper. aan de kop is breedte minder kritisch gezien er niemand naast je zit.

hier enkele versies met zitbreedte en beenruimte
4.803/1.663/125mm

2.500/2.500/250mm

3.200/3.200/320mm

3.200/3.200/150mm

Maar nu het geheel overbrengen op een tafel, liefst niet uit het handje. Dus toch die frees aan een lange stok/plank.

om een freespasser te maken vervang ik de voetplaat van de bovenfrees door een stuk melamine 8mm, dat glijdt lekker en met 8mm dikte hou je nog voldoende freesdiepte over. voor een tafel van 30-40mm dik moet je wellicht sowieso de laatste passen met een kopieerfrees doen.
goed nadenken over de freesrichting voor je begint (don't ask ...).
met stralen >2m lijkt een freespasser me dat toch wel een gedoe.
ik zou hier op veilig spelen en kiezen voor een kwart mal in MDF 9 of 12mm ipv rechtstreeks het tafelblad op vorm te frezen.
en, gezien de grote stralen, zou ik de mal tekenen met een touwtje, ruw uitzagen met de decoupeerzaag en verder op vorm schuren of schaven. met een bandschuurder is dat zo gebeurd.

 

[keesfrees]

Leuk en ook nog een recent, actief onderwerp waar ik "toevallig" op stuit nav een zoektocht waar bij ik de term "Deense ovaal" tegenkwam een term die ik nog niet kende.
Waarom ik daar wel benieuwd naar was is omdat ik regelmatig een vraag krijg voor freeswerk ( een mal of blad ) waar bij de meeste tijd gaat zitten in de c(r)ommunicatie over wat de aanvrager nu precies in het hoofd heeft qua vorm.
De term ovaal is nog al een breed begrip in de perceptie van velen. Vaak wordt een (wat ik maar ben gaan gebruiken) wielerbaan (of schaats, atletiek) bedoeld.
Twee halve cirkels met rechte stuken er tussen.
Maar, dit onderwerp zal ik onthouden (daarom regeer ik er ook in, gemakkelijker terugvinden) om als referentie te gebruiken bij toekomstige vragen op dit gebied.

O ja, nu ik er toch over bezig ben.
Bij het maken (tekenen) van boogsegmenten is het belangrijk dat ze tangent aansluiten, geen scherpe overgangen dus, dat zie ik nogal eens fout gaan, al dan niet door gebrek aan de juiste functie ( niet gebruik of ontbreken ).

En ( maar, ten overvloede ) een mooie mal te maken is een leuk klusje met een bovenfrees ( kopieerfrees met lager ) en wat dun plaat materiaal, bovenfrees met passerhulpstuk, enzzz.

 

[Guido76]

O ja, nu ik er toch over bezig ben.
Bij het maken (tekenen) van boogsegmenten is het belangrijk dat ze tangent aansluiten, geen scherpe overgangen dus, dat zie ik nogal eens fout gaan, al dan niet door gebrek aan de juiste functie ( niet gebruik of ontbreken ).


Ik snap dat de ene boog mooi vloeiend moet overlopen in de volgende boog, alsof het 1 natuurlijke cirkel is. Maar hoe bedoel je al dan niet gebrek aan de juiste functie?

 

[keesfrees]

Toen ik het opschreef bedacht ik al dat het vragen op kon roepen, ik kon zo snel geen betere tekst verzinnen.
Ik bedoel, in sommige cad software is er geen functie om 2 boogsegmenten tangent te verbinden, wel lijn en boog, dus dan met je met hulplijntjes aan de gang en dan moet je wel weten wat je doet.
Je kan wel/ook 2 bogen verbinden met een boog middels de afrond functie.
En het kan op een scherm er prima uit zien en dan worden onvolkomenheden cq details pas zichtbaar na het frezen :-/

 

[Bert Vanderveen]

Toen ik het opschreef bedacht ik al dat het vragen op kon roepen, ik kon zo snel geen betere tekst verzinnen.
Ik bedoel, in sommige cad software is er geen functie om 2 boogsegmenten tangent te verbinden, wel lijn en boog, dus dan met je met hulplijntjes aan de gang en dan moet je wel weten wat je doet.
Je kan wel/ook 2 bogen verbinden met een boog middels de afrond functie.
En het kan op een scherm er prima uit zien en dan worden onvolkomenheden cq details pas zichtbaar na het frezen :-/

Om mooie overgangen te krijgen is er de Bézier-methode, uitgevonden door een Franse ingenieur en in eerste instantie gebruikt bij het ontwerpen van carosserieën van auto’s (nu weet je waarom die vooroorlogse en iets latere Citroëns en Renaults zo fraai zijn). Zoek maar even op wiki wat het precies is, want qua wiskunde en zo ben ik een oen.

In mijn vroegere vak had ik met Bézier-curves te maken omdat die gebruikt werden in de software om lettertypen om te zetten naar digitale bestanden. Software die geleid heeft tot apps als Illustrator en Inkscape. De pagina-beschrijvingstaal PostScript maakt gebruik van de mathematische definities van dergelijke curves om met zo min mogelijk bits gecompliceerde vormen te beschrijven; de gemiddelde wereldburger heeft er dus dagelijks mee van doen…

In industriële ontwerpsoftware wordt inmiddels gebruik gemaakt van andere methodes omdat Béziercurves zich moeilijk laten vertalen naar 3-D, waar bijvoorbeeld nurbs beter werken - daarmee kun je ondanks lokaal ingrijpen in drie dimensies vloeiend blijven). Maar voor het ontwerpen van min om meer 2-D objecten leent het zich nog steeds voortreffelijk.

Met behulp van Béziercurves tekenen op de computer vergt enige ervaring - er zijn een aantal trucjes die helpen om mooie overgangen te krijgen. Een aantal van die handigheidjes heb ik verwerkt in mijn suggestie om met in vieren gevouwen karton het ontwerp te maken. Zoals het plaatsen van de controlepunten op de extremen van de vorm, het uitvloeien van overgangen door een zo vlak mogelijke aanloop, enzovoorts.

PS Mijn verhaal is natuurlijk wel een tikje jipenjanneke, dus zonder garantie. Wie er meer over wil weten vindt genoeg aanknopingspunten op het web met zoektermen uit dit epistel.

 

[keesfrees]

Ik weet helemaal wat je bedoelt, ik leg dat altijd uit door de vergelijking te maken met een slap latje door een aantal punten ( spijkertjes ).
Het probleem bij cnc frezen is dan de omzetting naar bogen want (bijna alle) cnc machines kennen alleen lijnen en bogen.
En het omzetten gaat wel eens mis, de definitie van de vele soorten slappe lijnen lijdt tot spraakverwarring ( zeg maar ) tussen de systemen, de lijnen corresponderen dan niet helemaal, daarom leg ik de omgezette lijn weer op het origineel.

Om mooie overgangen te krijgen is er de Bézier-methode, uitgevonden door een Franse ingenieur

Aha, dat wist ik dan weer niet, interessant.